The perspective transformation and collinearity

When working with the graphics pipeline, the perspective projection is commonly used to give a realistic depiction of a scene, where objects close to the camera appear larger than objects far away. The perspective transformation has the important feature of mapping 3D lines to 3D lines. In this post we will go into why this property is important and give a proof of it.

The reader should have some familiarity with the graphics pipeline and the role the projection transformation plays in it. The Sources section provides good resources on the subject.

Coordinates setup

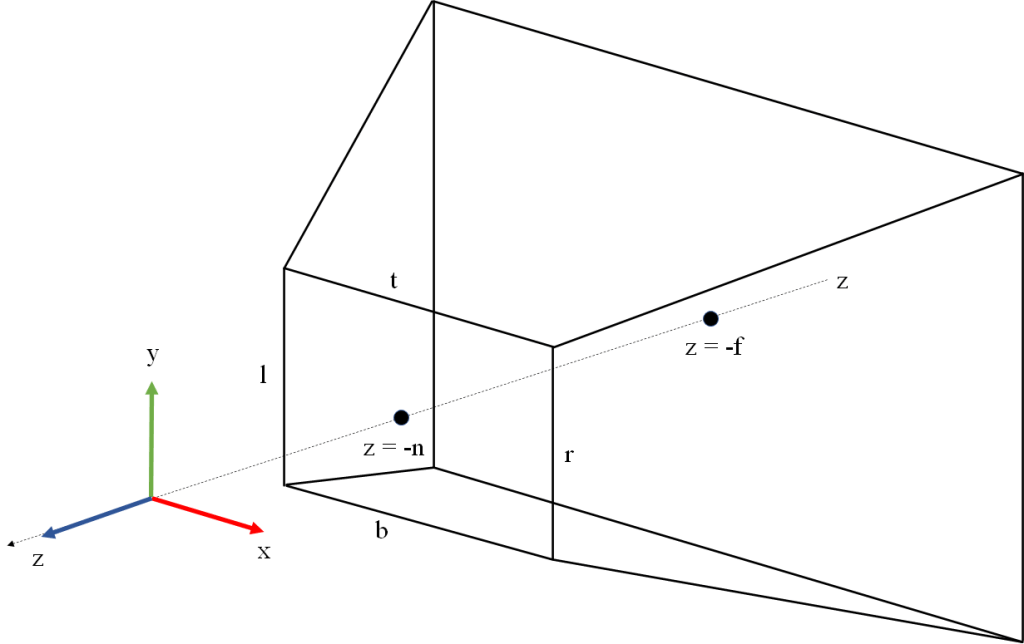
In the following we will assume that our view space is a right-hand coordinate system, has X pointing right from the camera, Y pointing up, and Z pointing back from the camera. This is the traditional setup of the view coordinate system in OpenGL applications.

Within the view space we define our viewing frustum by a near plane orthogonal to the Z axis placed at $z = -n$ , a far plane orthogonal to Z placed at $z = -f$ (so $n$ and $f$ are positive numbers). The near face of the frustum is delimited by X ranging from $l$ to $r$ , and Y ranging from $b$ to $t$ . Note this frustum is not necessarily symmetrical. In practice it is usual to use a symmetrical frustum, but this can be easily inferred as a special case. The view frustum is illustrated in Figure 1.

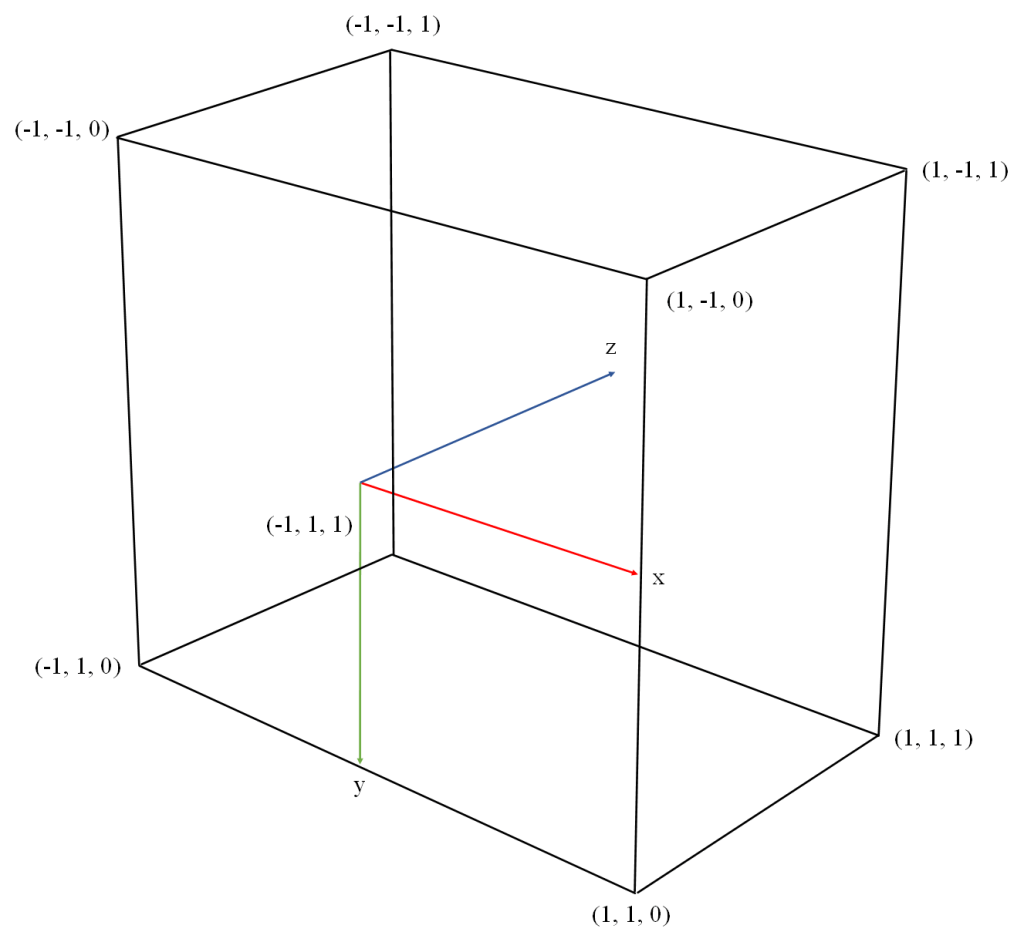
Our NDC (Normalized Device Coordinates) system will be right-handed with X pointing right, Y pointing down, and Z pointing into the screen. The canonical view volume is defined by X and Y ranging from -1 to 1, and Z ranging from 0 to 1. The canonical view volume is illustrated in Figure 2. This NDC setup is how Vulkan defines it in its spec.

Other rendering APIs use different NDC setups. OpenGL defines its NDC as a left-hand coordinate system, with X pointing right, Y pointing up, Z pointing into the screen, and all three coordinates ranging from -1 and 1. DirectX defines its NDC as left-handed, with X pointing right, Y pointing up, Z pointing into the screen, X and Y ranging from -1 to 1 and z ranging from 0 to 1.

We have defined our view coordinate system with the approach usually employed in OpenGL applications. This should be natural for those accustomed to working with this API, and also has the advantage that the Y axis points up allowing us to think of Y as “height”. Note however, that since the Vulkan NDC has Y pointing down and Z pointing in the same direction as the camera, we will need to define our projection transformation with negative coefficients in Y and Z, in order to flip the direction of these axes.

Figure 2. The canonical view volume in Vulkan NDC.

The perspective transformation

With the above coordinates setup (mapping z to the interval [0, 1]) the perspective transformation can be described by the following matrix:

$P = \begin{pmatrix} \frac{2n}{r-l} & 0 & \frac{r+l}{r-l} & 0 \\ 0 & \frac{2n}{b-t} & \frac{b+t}{b-t} & 0 \\ 0 & 0 & \frac{f}{n - f} & \frac{fn}{n - f} \\ 0 & 0 & -1 & 0 \end{pmatrix}$

Remember there is an implicit division by w after the matrix is applied. Note also that we have defined the fourth row of the matrix as $(0, 0, -1, 0)$ , so $w' = -z$ . That is to say, when we divide by w in clip space we are actually dividing by the view space $-z$ .

For a detailed derivation of this matrix, see Sources. The explanation in that page is oriented towards the OpenGL NDC system so the matrix they build is different from our Vulkan-oriented matrix, but they show a generic method that can be used to derive the perspective matrix with any NDC setup.

Projection and the graphics pipeline

As a reminder, the following is a simplified summary of the steps of the graphics pipeline in a typical application and the role the projection matrix plays in it. Some details like the orientation of the framebuffer coordinate system vary depending on the graphics API. This summary assumes we are working with Vulkan. For a more detailed description see Sources.

The model space coordinates of each vertex are input into your vertex shader.
Your vertex shader takes the model space coordinates of the vertex, converts them to homogenous coordinates by adding a w component with value 1, and multiplies the homogeneous vector by the 4×4 model matrix to obtain the world space coordinates.
The vertex shader takes the world space coordinates and multiplies them by the view matrix to obtain the view space coordinates.
The vertex shader takes the view space coordinates and multiplies them by the projection matrix P above to obtain the clip space coordinates. This is what the vertex shader returns. The vertex shader may combine the model, view an projection matrices into a single multiplication and return $P * V * M * v_{model}$ .
The clip space coordinates returned from the vertex shader are divided by their w component to obtain Normalized Device Coordinates (NDC). This step is sometimes called perspective division. This is a fixed function step.
The NDC are converted to framebuffer space (called window space in OpenGL) with an affine transform. The window space coordinates describe the vertex position in a coordinate system that has its origin in the top left corner of the window, and is scaled so that pixels have width and height 1 . This is a fixed function step.
Primitives are rasterized (converted to a set of samples called fragments). For each fragment, its barycentric coordinates are computed in framebuffer space, and then its framebuffer space coordinates $x', y', z'$ are computed by linearly interpolating the framebuffer space coordinates of the primitive vertices, using the barycentric coordinates of the fragment as weights. The framebuffer space z coordinate in particular is relevant because it will be used in the z test. This is a fixed function step.
The fragment’s vertex attribute values (e.g. texture coordinates) are computed via perspective-correct interpolation of the vertex attributes of the vertices. This involves using the view space (pre-projection) z values at the vertices. This is a fixed function step.
Early z test: if the driver and GPU support it (most do) and our pipeline doesn’t write to the depth buffer or use discard in the fragment shader, the pipeline will probably do the early z test at this point. The fragment’s z coordinate in framebuffer space is compared against the value stored in the depth buffer for the current pixel. If the fragment’s z is greater or equal than the value stored in the depth buffer, it means the fragment is occluded so it is discarded. Otherwise, the depth buffer is updated with the framebuffer z value of the fragment and processing of the fragment continues. This is a fixed function step.
Your fragment shader is invoked with the framebuffer space coordinates of the fragment as input.
If we have a stencil buffer attached, the stencil test is performed.
If the pipeline wasn’t able to do the early z test, z testing is performed at this point (late z test). Otherwise the late z test is skipped. The late z test involves the same read and possible write of the depth buffer described above in the early z test step.
The color returned from the fragment shader is written to the framebuffer.

The use of a depth buffer and a stencil buffer is optional in the graphics pipeline, but its use is so common that we have included it in the summary.

The collinearity property

The perspective projection doesn’t preserve parallelism. Parallel lines in view space get mapped to lines that meet in a point, the projection of which over the near plane is called their vanishing point.

Parallel lines are projected to lines that intersect at a vanishing point. Photo by Joshua Burdick on Unsplash

Lengths are not preserved either. Points get shifted inwards and backwards towards the far plane, and the farther from the near plane we go the more shifted they are. This generates the effect of far away objects looking smaller than objects of the same size that are closer to the camera.

However, the perspective projection as defined above has the important property that 3D lines in view space (after applying perspective division) get mapped to 3D lines in framebuffer space. Note we are not only talking about lines being mapped to lines in the projection plane: the 3D coordinates post projection also remain aligned, and this is important. For this reason we say that perspective is a projective transformation (it maps lines to lines, without preserving parallelism nor distances).

The key feature of the projection that is the cause of this property is the way the z coordinate is remapped in the third row of the projection matrix. When we look at the perspective matrix, we can see that after w division, the view space coordinates $(x, y, z)$ will be mapped to framebuffer space coordinates $(x', y', z')$ according to the following equations:

$x' = (\frac{2n}{r-l})\frac{x}{-z} - \frac{r+l}{r-l}$

$y' = (\frac{2n}{b-t})\frac{y}{-z} - \frac{b+t}{b-t}$

$z' = (\frac{fn}{n - f})\frac{1}{-z} - \frac{f}{n - f}$

Notice how $x'$ and $y'$ are hyperbolic functions of $z$ . If we had left $z'$ as a linear function of $z$ , our straight lines would turn into hyperbolas after projection. For a good graphical depiction of how this would look like, see Sources.

The mapping of $z'$ as another hyperbolic function of $z$ has the effect of compensating the curve of $x'$ and $y'$ and producing a straight line. Note this preserves collinearity, but not lengths: points that are equally spaced across the line in view space will get shifted along the line towards the far plane in a non linear fashion.

Remember that the graphics pipeline needs to determine the value of the framebuffer space z for each fragment, based only on the framebuffer space z values at the vertices of the primitive. This is done by doing a linear interpolation of the framebuffer space z values at the vertices (i.e. a linear combination of the vertices’ z values using the sample’s barycentric coordinates as weights). This is the reason the collinearity property is important: if straight lines in view space were turned into curves after projection, this linear interpolation would be impossible.

Note that here we are talking about the linear interpolation of the framebuffer space z values, which is used in depth testing to discard occluded fragments. This should not be confused with the perspective-correct interpolation of vertex attributes, which is done using the clip space w (which takes the value of the pre-projection view space -z) and is therefore independent of how the projection remaps z.

Formal statement of the collinearity property

For the purposes of stating the collinearity property in formal terms, there is an important observation that will allow us to present the theorem in a more simple and elegant way. Note that the way we have defined the perspective projection can be divided in two steps:

Dividing input coordinates by $z$ to make far away objects look smaller (projective component).
Multiplying by scalars and adding scalars in order to adjust the ranges and orientations of $x'$ , $y'$ and $z'$ to those expected by NDC (affine component).

The affine component doesn’t affect collinearity (we already know it will map lines to lines due to it being an affine transformation ). In order to prove that perspective maps lines to lines, it’s enough to show that the projective component does. Note that the projective component doesn’t need to flip Y or Z, this is part of the job of the affine component.

Theorem. Let $A = (x_A, y_A, z_A)$ and $B = (x_B, y_B, z_B)$ be two points in $\mathbb{R}^3$ , and $S = \frac{A + B}{2}$ their mid point. We define a perspective transformation as the function $f : \mathbb{R}^3 \rightarrow \mathbb{R}^3$ defined by the formula $f(x, y, z) = (\frac{x}{z}, \frac{y}{z}, \frac{1}{z})$ . Let $A'$ , $B'$ and $S'$ be the images of $A$ , $B$ and $S$ through $f$ respectively. Then the point $S'$ lies on the line segment $\overline{A'B'}$ . This is to say, there exists a $\lambda \in \mathbb{R}$ such that $S' = \lambda A' + (1 - \lambda) B'$ .

Proof

From the definition of $f$ we have:

$A' = (\frac{x_A}{z_A}, \frac{y_A}{z_A}, \frac{1}{z_A})$

$B' = (\frac{x_B}{z_B}, \frac{y_B}{z_B}, \frac{1}{z_B})$

$S' = (\frac{x_A + x_B}{z_A + z_B}, \frac{y_A + y_B}{z_A + z_B}, \frac{2}{z_A + z_B})$

We can separate $S'$ as:

$S' = (\frac{1}{z_A + z_B})(x_A, y_A, 1) + (\frac{1}{z_A + z_B})(x_B, y_B, 1)$

$S' = (\frac{1}{z_A + z_B}) z_A (\frac{x_A}{z_A}, \frac{y_A}{z_A}, \frac{1}{z_A}) + (\frac{1}{z_A + z_B}) z_B (\frac{x_B}{z_B}, \frac{y_B}{z_B}, \frac{1}{z_B})$

$S' = (\frac{z_A}{z_A + z_B}) (\frac{x_A}{z_A}, \frac{y_A}{z_A}, \frac{1}{z_A}) + (\frac{z_B}{z_A + z_B}) (\frac{x_B}{z_B}, \frac{y_B}{z_B}, \frac{1}{z_B})$ (1)

If we denote $\lambda = \frac{z_A}{z_A + z_B}$ then it’s easy to see $\frac{z_B}{z_A + z_B} = 1 - \lambda$ . So we can rewrite equation 1 as:

$S' = \lambda A' + (1 - \lambda) B'$

$\square$

Alternative proof

The book “3-D Computer Graphics A Mathematical Introduction with OpenGL” by Samuel Buss provides an alternative proof, with a more generic statement. The proof can be found in chapter II “Transformations and Viewing”. The argument in broad strokes is the following.

Consider any function $f : \mathbb{R}^3 \rightarrow \mathbb{R}^3$ that can be represented by a 4×4 matrix. Given an input point $P \in \mathbb{R}^3$ , its representation in the 3-dimensional projective space is a line through the origin in $\mathbb{R}^4$ . If $P$ varies on a line in $\mathbb{R}^3$ then its projective representation spans a plane through the origin in $\mathbb{R}^4$ (i.e. a 2-dimensional subspace). The image of this subspace by the matrix is another subspace whose dimension cannot be greater than 2. There are three possible cases then:

The image subspace is of dimension 0. Then the function is not defined for the point $P$ .
The image subspace is of dimension 1. Then its points represent a point in $\mathbb{R}^3$ (this is what happens for example when we try to project a point that lies on the plane through the eye parallel to the near plane, the result is a point at infinity).
The image subspace is of dimension 2. Then its points represent points in $\mathbb{R}^3$ that vary over a line.

Sources

About the derivation of the perspective matrix in OpenGL: https://www.scratchapixel.com/lessons/3d-basic-rendering/perspective-and-orthographic-projection-matrix/projection-matrix-introduction.html
Stackoverflow answer showing a graphical comparison between linear and hyperbolic mapping of z: https://stackoverflow.com/questions/47801957/linear-depth-buffer/47802596#47802596
Buss, Samuel R. “3-D Computer Graphics A Mathematical Introduction with OpenGL”. Provides an alternative and more generic proof of the property that perspective maps 3D lines to 3D lines.
About the rasterization algorithm and linear interpolation of z values: https://www.scratchapixel.com/lessons/3d-basic-rendering/rasterization-practical-implementation/visibility-problem-depth-buffer-depth-interpolation.html
About perspective-correct interpolation of vertex attributes: https://www.scratchapixel.com/lessons/3d-basic-rendering/rasterization-practical-implementation/perspective-correct-interpolation-vertex-attributes.html
Low, Kok-Lim. Perspective-Correct Interpolation. This is another in-depth article about the subject: https://www.comp.nus.edu.sg/~lowkl/publications/lowk_persp_interp_techrep.pdf
Another explanation about perspective-correct interpolation in Stackoverflow: https://stackoverflow.com/questions/24441631/how-exactly-does-opengl-do-perspectively-correct-linear-interpolation
About the stages of the graphics pipeline: https://www.khronos.org/opengl/wiki/Rendering_Pipeline_Overview
Wikipedia on projective transformations: https://en.wikipedia.org/wiki/Homography